Практичне заняття №1 Тема: Множини. Числові множини

роблю завдання на замовлення- звертайтесь. Зв’язатися зі мною ви можете у коментарях

Практичне заняття №1

Тема: Множини. Числові множини

1. Теоретичні питання
   1. Поняття про множину. Елементи множини. Запис множин та їх елементів. Скінченні і нескінченні множини. Приклади множин.

Основні числові множини.

2. Геометрична фігура, як множина точок. Круги Ейлера.
3. Способи задання множин. Порожня і одинична множини.
4. Рівність множин.
5. Означення підмножини множини. Відношення включення множин та його властивості.
6. Види підмножин множини.
7. В яких відношеннях можуть знаходитись дві множини?
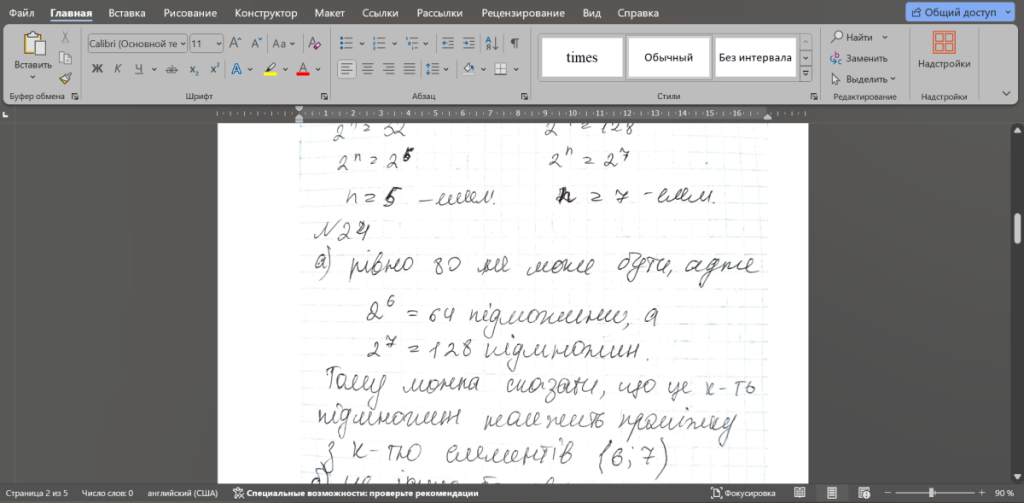
8. Множина всіх підмножин множини. Скільки підмножин у 5елементної множини? Універсальна множина та її зображення.

2. Задачі для розв’язування.

2. Задачі для розвʼязування.
1. Які назви використовують для означення:
множини тварин;
множини військовослужбовців?
Як називають множину всіх:
а) артистів, що працюють в одному театрі; б) точок земної поверхні рівновіддалених від одного з полюсів;
в) точок земної поверхні рівновіддалених від обох
полюсів?
2. Серед заданих множин вказати рівні:
C = 19.6,31:
A-********* F860
К = 13. 6. 21.
3. Сероможи охочанти пороріними протилежними
сторонами;
В- мноина примкунікі сленких нарианаються
в різних точках:
Д – множина цілих коренів рівняння 2х + 5х – 12 = 0.
а) Задати переліком елементів множину натуральних чисел – дільників числа 36;
б) чи можна задати переліком елементів множину натуральних чисел, які кратні 36?
в) задайте дві попередні множини за допомогою характеристичних властивостей їх елементів.
Серед даних множин вказати скінченні і нескінченні.
множина простих чисел;
множина парних чисел;
множина студентів університету;
множина розвʼязків нерівності
множина теорем, доведених у підручнику з геометрії

множина теорем, доведених у підручнику з геометрії
для 7 – 11 кл.;
б) множина цілих дільників числа 144;
множина точок прямої;
множина цілих чисел, які діляться на 3;
множина коренів рівняння х + 1 = 0.
6. Нехай М = {3}]. Який із записів правильний:
13} €M;
{3} C M?
7. Назвати власні підмножини множини:
паралелограмів;
трикутників;
натуральних чисел.
8. Відомо, що А с Ві а є А. Які з тверджень істинні:
2) a * B?
9. Відомо, що А с В і вє В. Що можна сказати про істинність тверджень:
1) 6 € A;
2）6EA？
10. Ne7. [8, с. 7).Задати числову множину описом
характеристичної властивості елементів:
a) 13; 8[;
B)]- ∞;-3];
6）］-∞；7
r) [-5,2; 0];
д) [-8;+ ∞ [;
e) 12,7; +∞ [;
2
*) [0; 7,8[;
3）］-4:8］.
11. Ne9(8, с. 7]. Прочитати наступні висловлення і вкажіть серед них істинні:
a) 3 € ]3; 12];
6)- 0,2€ [-0,3; 0];
6) 0€ ]-∞; 0];
2) 5 € ]6; +∞ [: 0) 75 € 0:
e) 6,4 € Z,
ж) – 7 € N;
3) 0,3 € Z.
12. Nº14 [8, с. 9]. Встановити у якому віднощенні знаходяться множини А і В, якщо А = (a, b, c, d), а
множина В така:

13. Nº 15[8, с. 9]. В якому випадку множини С і D
перстинаються:
а) С – множина парних одноцифрових чисел.
D – множина непарних одноцифрових чисел; б) С – множина парних одноцифрових чисел,
D – множина чисел, кратних 3:
в) С – множина прямокутних трикутників,
D – множина рівнобедрених трикутників; г) С – множина прямокутників з рівними сторонами.
D – множина квадратів?
14. Nº 16[8, с. 10]. Зобразити за допомогою кругів Ейлера множини Р і Q, якщо Р – множина рівнобедрених трикутників, а О є множиною:
а) гострокутних трикутників;
6) прямокутних трикутників;
в) рівностороних трикутників.
Nº 17[8. с. 10]. Дано множину С = (213. 45. 324. 732.
136}. Записати підмножину множини С, що складається із чисел, які:
а) діляться на 3;
б) діляться на 9; в) не діляться на 4; г) діляться на 5.
Ne 18 [8, c. 10]. А – множина прямокутників, D –
множина
квадратів. Довести,
що множина
D
підмножиною множини А та зобразіть дані множини за допомогою кругів Ейлера.
17. Nº 19 [8, c. 10]. А – множина паралелограмів, В – множина прямокутників,
С – множина квадратів.
Довести, що А с В і В с С. Зобразити дані множини за допомогою кругів Ейлера.
18. Ne 20 [8, c. 10]. Показати, використовуючи круги Ейлера, що якщо В с АСс В, то А с С.3. Домашнє завдання
Nº 21[8, с. 10]. Дано множину М = {k, I, m}. Записати всі її: а) одноелементні підмножини; б) двохелементні підмножини; в) трьохелементні підмножини.
Приєднайте до отриманих пдмножин порожню множину. Скільки всього підмножин отримали?
Nº 22[8, с. 10]. Записати всі підмножини множини К = (р, r,
s, [}. Скільки їх вийшло?
Nº 23[8, с. 10]. Скільки елементів у множині, яка має 32
підмножини? 128 підмножин?
Nº 24[8, с. 10]. Чи існує така множина, яка: а) має всього 80
підмножин? 0) не має жодної підмножини?
Nº 25[8, с. 10]. Відомо, що N – множина натуральних чисел,
7 – множина цілих чисел. Довести, що висловлення
Z c N хибне.
Nº 26[8, с. 10]. Зобразити за допомогою кругів Ейлера, що
NcZiZc Q. Чи правильно, що Q с R?
Nº 27[8, c. 10]. А – множина натуральних чисел, менших 20;
В, С, D і E – підмножини множини А, такі, що В складається з чисел, кратних 6, С – із чисел, кратних 2,
D – із чисел, кратних 3, Е – із чисел, кратних 2 і 3
одночасно. Перерахувати елементи множин В, С, D i E
і вказати серед них рівні множини.
No 28[8, c. 10].
M –
множина натуральних розвʼязків
нерівності 2 ≤ х < 7.
множина
розвʼязків нерівності
Які
натуральних наступних
висловлень істинні: а) М с К; б) К с М; в) М = К?
Ne 30[8, c.
10. А – множина двецифрових
чисел;
множина парних натуральних чисел; С
– множина
натуральних чисел, кратних 4. В якому із випадків, зображених на малюнку, зображені дані множини?
Навести приклади
мноЖин Л, В і С.
якщо
зображення таке як на мал. в)

Nº 29[8, с. 10]. Довести, що А = В, якщо:
а) А – множина двоцифрових чисел, кратних 9, В – множина двоцифрових чисел, сума цифр яких кратна
9;
6) А – множина натуральних чисел, запис яких
закінчується нулем, В – множина натуральних чисел,
кратних 10.

3. Домашнє завдання

Рекомендована література

Автор / продавецьВсі товари продавця

Офлайн 15 години

Вчитель - розробник

Переглядів: 72

Потрібна допомога з навчанням? Я допоможу вам із рефератами, статтями, курсовими, практичними роботами та іншими академічними завданнями! Зв'яжіться зі мною через коментарі на сайті, і ми разом досягнемо успіху в навчанні.

Коментарі: 4Публікації: 297Реєстрація: 20-02-2024

Посада: ВчительПрофесійні навички: